有趣筆記

2016年5月15日星期日

Feature extraction, feature selection, model selection

feature extraction：現實生活不是任何資料都可以直接交給model處理，需要透過適當的處理
feature selection：feature不是愈多愈好，適當挑選feature可以提升model的準確度
model selection：對於不同的問題與資料，有不同適用的模型

feature extraction包含了兩個步驟，obtain features跟convert features
代表了如何處理各種資料方式，比方說要把圖片視為一維或者二為的資料呢?又或者透過統計學的方式，取得適當的資料型態，跟著或者可能使用one hot encoding編譯取得資料
其中有相當的部分是data preprocessing的範疇

feature selection必須考量到資料的與模型之間的適應性，捨棄一些太過正相關的資料，比方說用人名來作為是否會生存下來的依據，本身會有overfitting的問題。其次必須考量performance，為了現實的使用，適度的資料篩選來提升準確度是必要的
如果有無限的時間，或許我們可以嘗試使用所有排列組合，來挑選最佳的準確度的feature set，但是如果沒有那麼多時間，或許可以考慮使用統計學的方式，例如$\chi^2$來作為預測，經過一些實驗，大多數的狀況會發現，feature 個數在挑選若干個之後，準確度會開始收斂，所以適當的挑選feature是必須的

model selection，其實這是一個大哉問，有時候model的挑選是必須經過經驗的累積或者其他的人努力，比方說過去text classification曾經是兩大勢力，decision tree與naive bayes的爭奪戰，找出一個很良好，很大的syntax or semantic tree來的好呢？還是naive bayes的機率模型好，目前來說naive bayes已經成為了主流
選定model之後，另外一個問題就是hyperparameters，也就是模型的參數調教，比方說naive bayes有個$\alpha$如何挑選？或者SGD也有一個$\alpha$
如果在空間與時間的許可下，對特定問題的資料，做反覆的實驗，選定適合的$\alpha$ value，但是如果說問題的資料特徵一直隨時間變動，或許採用別種模型會比較合適

2016年5月14日星期六

Data Preprocessing, Naive Bayes, ID3, C4.5, Decision Tree

Data preprocessing是處理現實資料一些問題或者因應一些演算法的限制產生的技巧
比方說missing value，現實生活上，可能會有資料遺失的問題，就好筆填寫表格，有些欄位並沒有被填寫，如果以real value來說，就可以考慮使用現有的training set中的mean value來填入

在Text mining中，常用的演算法是naive bayes

例如想使用幾個關鍵字，代表某一個網頁，如果直接使用該網頁最常出現的文字來代表，會產生一種偏差，比方說am, are, he, she這類常見的文字

所以有一種稱之為Term Frequency Inverse Document Frequency(TF-IDF)的技巧，就是將所有要評估的網頁作單一文字，如果一個關鍵字在各個網頁出現在多次，那麼表示這個關鍵字是一個常見的文字，並不適合用來代表某個網頁

經過這樣的事先處理，就可以把文字丟入naive bayes演算法做計算，獲得比較好的分類器

而許多分類器只能接受數值型(numeric)的特徵，那麼就必須把category的特徵做轉換，如果只有單純的性別，就可以轉換為0跟1即可，如果類似居住城市這種多種類別，也可以轉換為0, 1, 2, ...。如果同時考慮多個category的特徵，是否可以使用一個數值來表示呢?這就是one hot encoding的方式，他將一個有m個可能性的category變成一個m個bits表達的數字，接著如果有k個特徵，整個可以變成k*m的binary數值，k個特徵只要經過一次numeric處理提升了分類器的效能，同時又兼顧了每個特徵的獨特性。

其實我認為one hot encoding是否能夠滿足分類器的需求，還是硬將category的特徵轉換為數值，對於提升分類的準確度的幫助才是整個重點

反過來，有些演算法卻只能比較有效處理category的特徵，好比ID3這種decision tree的演算法。它使用entropy/information gain來作為分類的標準，如果撇開數學意義來說，我個人以不嚴謹的白話說法就是，一個特徵對於target的辨識程度
https://en.wikipedia.org/wiki/ID3_algorithm

當然相對的來說，數值的轉換就是另外一道課題，好比ID3的改良C4.5就考慮到這一點。它使用若干個threshold來分隔數值
https://www.jair.org/media/279/live-279-1538-jair.pdf

相關資料
https://read01.com/5M32Jn.html
http://mirlab.org/jang/books/dcpr/prNbc.asp?title=5-5%20Naive%20Bayes%20Classifiers%20(%B3%E6%AF%C2%A8%A9%A4%F3%A4%C0%C3%FE%BE%B9)&language=chinese
https://zh.wikipedia.org/wiki/%E5%86%B3%E7%AD%96%E6%A0%91

2016年5月13日星期五

Bias-Variance Tradeoff

Bias-Variance Tradeoff比較接近一般的原則
但是以MSE來舉例比較容易觀察
https://en.wikipedia.org/wiki/Mean_squared_error
可以想像得到

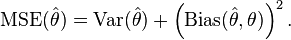
\operatorname{MSE}(\hat{\theta})=\operatorname{Var}(\hat{\theta})+ \left(\operatorname{Bias}(\hat{\theta},\theta)\right)^2.

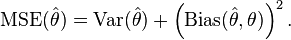
如果估計值越接近最小平分解的部分bias會最小，但是variance會放大，反之亦然
更多可以參考
http://blog.sciencenet.cn/blog-430956-768356.html

對於此原則與overfitting underfitting的交織結果
http://www.cnblogs.com/TenosDoIt/p/3712590.html
https://www.zhihu.com/question/27068705
https://cg2010studio.com/2012/10/29/%E5%81%8F%E5%B7%AE%E5%92%8C%E8%AE%8A%E7%95%B0%E4%B9%8B%E6%AC%8A%E8%A1%A1-bias-variance-tradeoff/

2016年5月12日星期四

Stochastic gradient descent(SGD)

中文有人翻譯為梯度下降法
考量一個線性回歸
$h_\theta = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \ldots = \sum_{j = 0} ^{l} \theta_j x_j$
cost function定義為
$J(\theta) = \frac{1}{2} \sum_i | y^{(i)} - h_\theta (x^i )|^2$
透過$\alpha$參數調整
$\theta_j \rightarrow \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta) \tag{1}$
$\alpha$參數是每次推估的差異性，太小可能收斂太慢，太大可能難以收斂

每次可以慢慢逼近最佳解
SGD的本質是最小平方解，但是好處是非常的實務
SGD本身的問題就不介紹了，如會陷入local optimal

SGD適用的範圍有幾個
1. data set很大的時候，可以使用SGD對data set做分割，有效率的進行
2. data set隨環境變化，例如隨時間變化，問題本身的最佳解隨時間推移，local optimal solution更貼切

SGD的特性
如果問題本身是qudraic convex問題，那麼他一定可以貼近最佳解（為何說貼近，因為是計算機本身計算誤差以及必須要在有限時間內找出解答，如果有無限時間應該可以收斂到最佳解。）

在blog上面寫數學式 -- MathJax

$\LaTeX$
$ x = {-b \pm \sqrt{b^2-4ac} \over 2a}. $
參考
http://note-on-cat.blogspot.tw/2013/07/mathjax-blogger.html

2016年5月11日星期三

Normalization

scaler=preprocessing.StandardScaler().fit(X_train)
X_train=scaler.transform(X_train)
X_test=scaler.transform(X_test)

sklearn提供了preprocessing的功能，最常見的就是normalization，對於不同scaler的資料提供一個可以比較的基礎
比較有趣這裡是使用了training資料當基礎，同時應用於test set上面

2016年5月9日星期一

開站囉

記錄一些資料的筆記
ipython3比python shell容易使用的shell替代品
不只可以使用[tab]自動補完，還可以將過程存檔
存檔指令%hist -f filename.py
附加指令%save -a filename.py 1-20

底下是一個嘗試的script



from sklearn.cross_validation import train_test_split

from sklearn import preprocessing

from sklearn import datasets

iris=datasets.load_iris()

X= iris.data[:, :2]

y=iris.target

X_train, X_test, y_train, y_test=train_test_split(X, y, test_size=0.25, random_state=33)

print(X_train.shape, y_train.shape)

scaler=preprocessing.StandardScaler().fit(X_train)

X_train=scaler.transform(X_train)

X_test=scaler.transform(X_test)

import matplotlib.pyplot as plt

colors=['red', 'greenyellow', 'blue']

for i in range(len(colors)):

    xs=X_train[:,0][y_train==i];

    ys=X_train[:,1][y_train==i]

    plt.scatter(xs, ys, c=colors[i])

  

plt.xlabel('Sepal length')

plt.ylabel('Sepal width')

plt.show()

2016年5月15日 星期日